2023四川达州中考压轴题详解

(四川达州中考)在△ABC中，AB=4

，∠C=60°，在边BC上有一点P，且BP=

AC，连接AP，则AP的最小值为_______

如第一个图所示，以BP为边，向右作△PBD，使△BPD~△ACB，相似比为1：2，故BD=2

，而∠BPD=∠ACB=60°，点P的轨迹为圆，圆心为O，且BO=2；明显，当A、P、O共线时，AP取最小值，∠PBD=∠CAB,得∠ABD ∠ABC=120°，而∠OBD=30°，故∠ABO=90°，AO=2

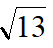
，故AP的最小值为2

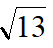
-2

点评：此题的核心的是找到点P的运动轨迹，通过相似、全等去转化线段是关键方法.以上方法供同学们参考.

(2023四川达州中考)(1)如图①，在矩形ABCD的AB边上取一点E，将ADE沿DE翻折，使点A落在BC上的A′处，若AB=6，BC=10，求

的值；

(2) 如图②，在矩形ABCD的BC上取一点E，将四边形ABED沿DE翻折，使点B落在DC的延长线上B′处，若BC·CE=24，AB=6，求BE的值；

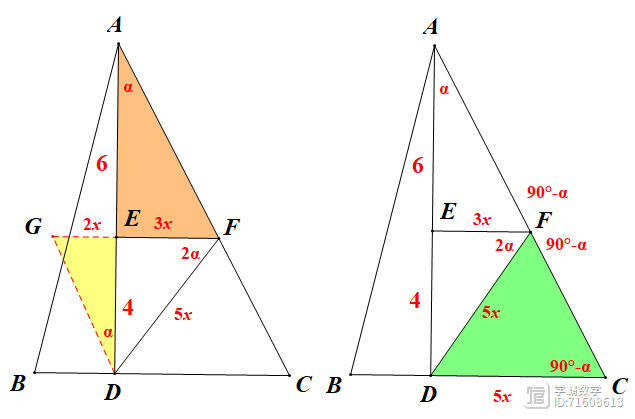
(3) 如图③，在ABC中，∠BAC=45°，AD⊥BC，垂足为点D，AD=10，AE=6，过点E作EF⊥AD交AC于点F，连接DF，且满足∠DFE=2∠DAC，直接写出BD

EF的值.

解：(1)由折叠的性质知A′D=AD=10，故AC=8，得AB=2，设AE=a，则AE=a，BE=6-a,由勾股定理得

得a=

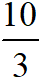
可得

(2) 易知△A′B′D~△CEB′，得

，而A′D=BC，A′B′=6得CB′=4，得A′D=8，故BC=8，由此可得BE=5

(3) 方法1：构造等腰三角形△DFG，使FG=FD，易知△DEG~△AEF，设GE=2x，则EF=3x，则DF=5x，易知x=1,故DF=CD=5；

方法2：设∠CAD=ɑ，则∠DFE=2ɑ通过标记角度易知∠DCF=∠DFC=90°-ɑ，得CD=DF，而EF：CD=3：5，设EF=3x，则DF=5x，得x=1,故CD=5

第二步：求BD，

方法一：将△ABD沿AB翻折得△ABG，将△ACD沿AC翻折得△ACI，延长GB、IC交于点H，易知AGHI为正方形，设GB=m，则BD=m，BH=10-m；由勾股定理得

得m=

，而CD=

EF故BD

EF=BC=

方法二：由12345原理知tan∠CAD=

,而∠CAD ∠BAD=45°，得tan∠BAD=

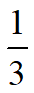
，故BD=

，而CD=

EF故BD

EF=BC=

点评：第三问的二倍角关系，一般会同步出现等腰三角形，通过直接构造等腰三角形，或者通过标记角度直接得到等腰三角形都可解决；难点在求解BC长度这个部分，12345原理是较快的，而半角模型的原始题能联想起来也是可以快速解决的.

12345原理，初中平面几何不得不说，掌握好可以秒解很多题目

半角模型深入研究，结论众多，逐一证明！

平面几何经典题，学霸数学老师历经一年时间整理成书，包含220多道经典题和详细答案，题目答案尽量做到详细和一题多解。当然，要消化这些题目，对同学们的要求较高，没有一定的基础，不建议深研和使用。感兴趣的小伙伴们可以扫下面小程序进入学霸数学小店购买。学霸数学老师每天会分享一道平面几何经典题，希望同学们关注并转发，让更多的人看到精彩的内容，这是学霸数学老师的动力。

关于学霸数学

＂学霸数学＂专注于数学中考高考考试的最新信息，好题与压轴题解题技巧、知识专题分析以及考试分析与解答，考试动向及政策分析解读、家庭教育相关分享！如果您是家长或学生，对学习方面有任何问题，请联系小编！