趣味几何 | 三角形中的角格点问题

定义：如果三角形的三个角的度数都是10°的整数倍,三角形内一点与三角形的三个顶点分别联结后，得到的所有的角也都具有这个性质，我们称这样的点为三角形中的角格点.

一题多解｜再看构造等边三角形的妙用

一题多解｜5种辅助线求解等腰三角形角度

之前写过两篇解题的方法，其实本质上就是三角形的角格点问题，今天我们深入的来研究一下角格点问题。

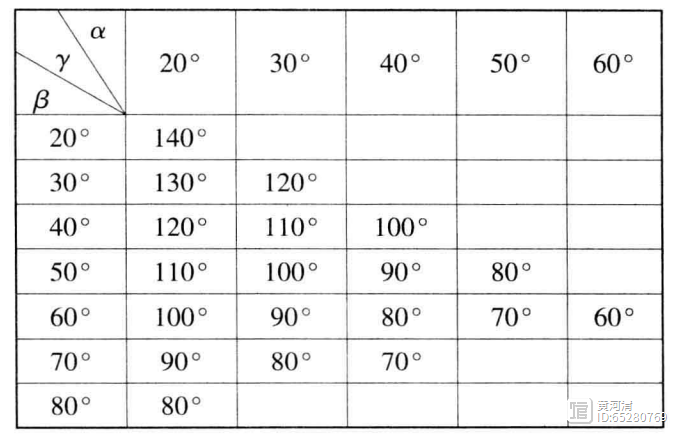
由于三角形的三个内角之和为180°，要使其中存在角格点，必要条件是每个角的度数都局限在20°30°,40°…,140°这13个度数之内，而不能是10°、150°、160°或170°，这是因为若有一个角是10°，则其中没有角格点；若存在两个角都不小于20则第三个角不大于140°。三个角都是10°整数倍的三角形共有27种(即 A B C=18,A≥B≥C的正整数解)，其中8种包含10°角的，肯定没有角格点，故可能存在角格点的三角形有19种，即三内角α，β，γ满足α≤β≤y时有下表：

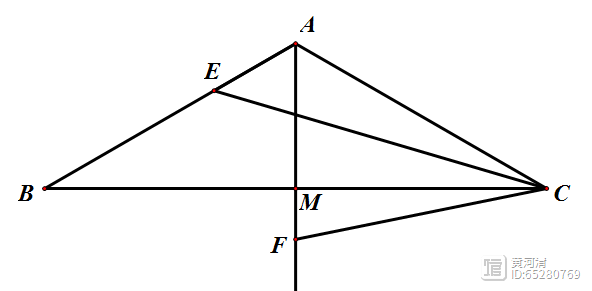
辅助线做法：构造等边三角形。我们通过一道题的角度变化来看一般性的辅助线做法。

1、在△ABC中，∠ABC=30°，∠ACB=20°，P为三角形内一点，∠PBC=20°，∠PCB=10°，求∠PAB的度数.

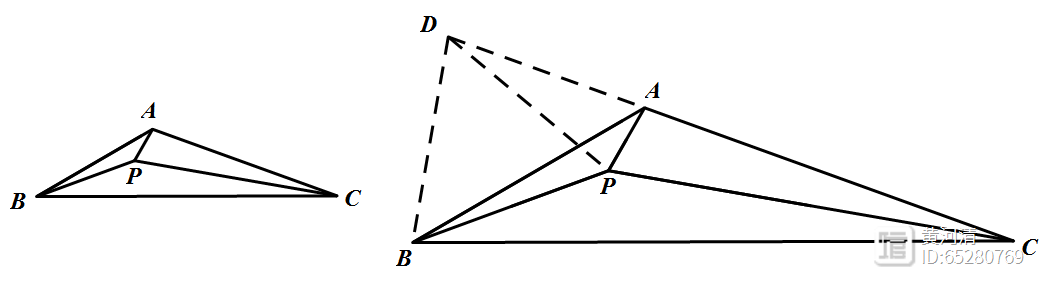
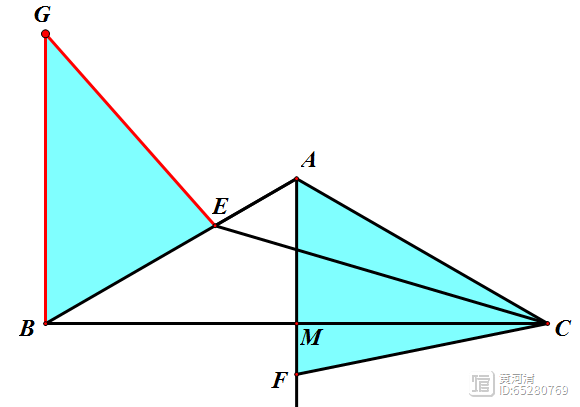
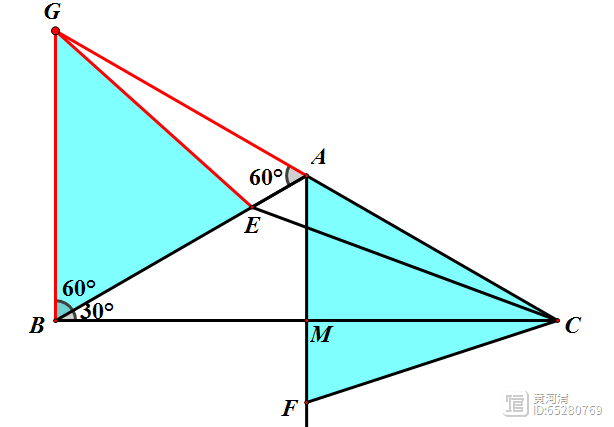
辅助线：以PB为边向外作等边△PDB。

结合以上角度计算，我们可以得到点B与点D关于直线PC对称。

连接DC，根据对称的性质，我们可以得到：∠CDP=∠CBP=20°，则∠BDA=80°；在△DBA中，∠DAB=50°；又因为∠BAC=130°，则D、A、C三点共线；

我们又可求得：DB=DA=DP，所以△DAP为等腰三角形所以∠DAP=∠DPA=80°所以∠BAP=30°2、在△ABC中，∠ABC=30°，∠ACB=20°，P为三角形内一点，∠PAB=30°，∠PCB=10°，求∠PBC的度数.

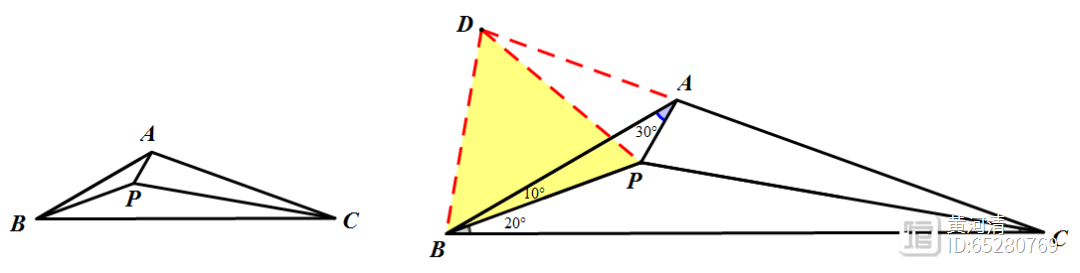
辅助线：以AB为边向下作等边△ADB。

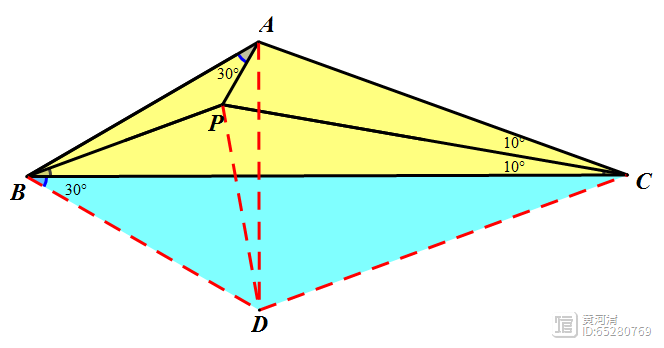
由等边三角形ABD和∠ABC=30°得到∠CBD=30°，从而△ABC≌△DBC所以∠DCB=∠ACB=20°所以∠PCD=∠PAD=30°（对应弦PD）

所以A、P、D、C四点共圆

所以∠PDA=∠ACP=10°（对应弦AP）我们容易证得△ABP≌△ADP所以∠PDA=∠PBA=10°所以∠PBC=20°3、在△ABC中，∠ABC=30°，∠ACB=20°，P为三角形内一点，∠PAB=30°，∠PBA=10°，求∠PCB的度数.

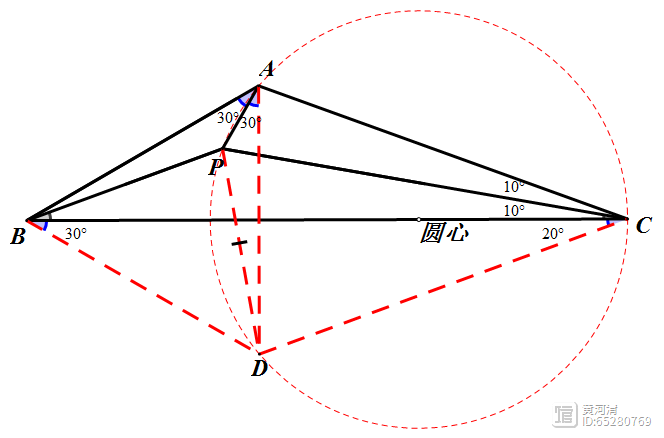
辅助线：以BP为边向左作等边△PDB。

①∠PAB=30°，∠PDB=60°，A、B、P三点共圆，圆心为D；②DB=DA，则∠DBA=∠DAB=50°，则D、A、C三点共线；③DB=DA=DP，三角形DAP为等腰三角形，所以∠ADP=20°，∠CDB=∠CBD=80°④易证∠CDP≌∠CBP，所以∠DCP=∠BCP=10°

后语：关于辅助线的构造，一方面可以构造等边三角形，但是以哪条边往哪个方向作等边三角形，需要大家思考积累经验；二方面也可以用对称的性质构造辅助线；