来解题吧 | 再看“逆等线”求最值

原题重现：在△ABC 中，AB＝AC，点 E 为边 AB 上一点，连接 CE．若 ∠BAC＝120°，过点 A 作直线 AM⊥BC 交 BC 于点 M，点 F 为直线 M 上 一点，BE＝AF，连接 CF，当 CE CF 最小时，直接写出∠ECF 的度数。

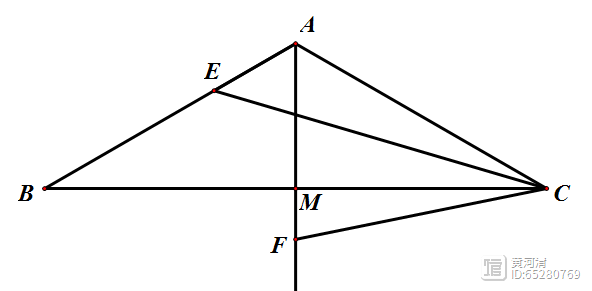
思路分析：首先我们通过题目条件判断，一个定点，两个动点（在两条定直线上运动），这不是“将军饮马”的基本题型；然后我们发现两个动点在运动过程中，始终保持等线段关系（BE=AF）；最后我们想到这是“逆等线”问题，所以利用逆等线构造全等三角形进行线段的转换。

解题回顾：

来解题吧 | 逆等线，构全等，求最值

来解题吧 | 加权逆等线，构相似，求最值

同学们再看看上面这两道题的解题思路，那么这道题也就迎刃而解了。

解题步骤：

（1）利用“两点间线段最短”将线段CE和CF的位置关系进行转换。

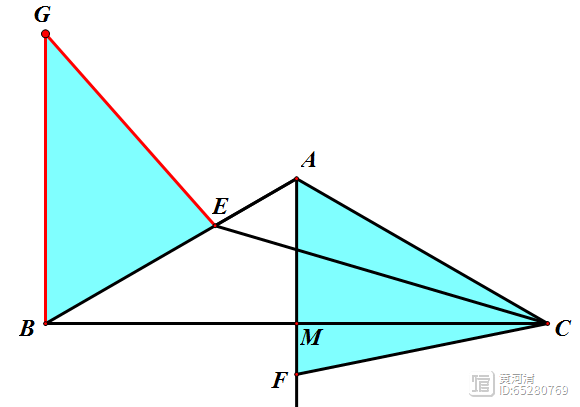
因为∠FAC=60°为定值，AC为定长，所以作∠EBG=∠FAC=60°且GB=AC，则△GBE≌△CAF；此时CF=GE，则CE CF=CE GE；

（2）当G、E、C三点共线时，CE CF取得最小值等于GC的长度；

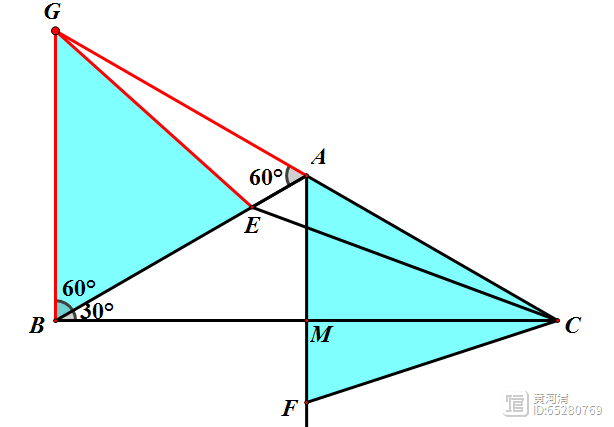
（3）我们可以得到△GBA为等边三角形，所以∠GAC=60°，又因为∠BAC=120°，则G、A、C三点共线。又因为E在AB上运动，所以当GEC三点共线时，点E与点A重合。

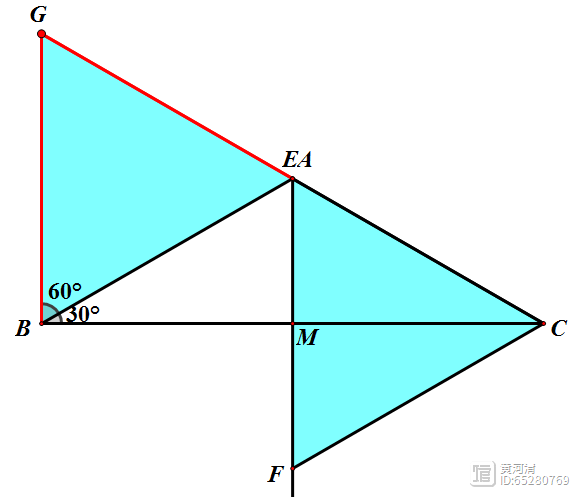
（4）此时，我们容易得到△ECF为等边三角形，所以∠ECF=60°。

补充解题：

（1）作A关于直线BC的对称点G，利用等边三角形的性质，将BE=AF，转化为AE=GF，从而得到△GAE≌△CGF；所以CF=GE；

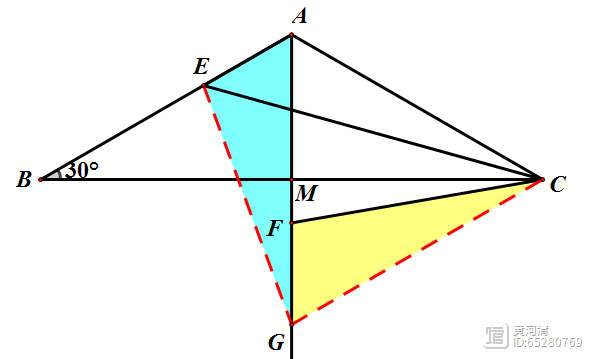
（2）将“逆等线”问题转化为将军饮马问题，此时CE CF=CE GE，C、G为定点，E为动点（E在定直线AB上运动）

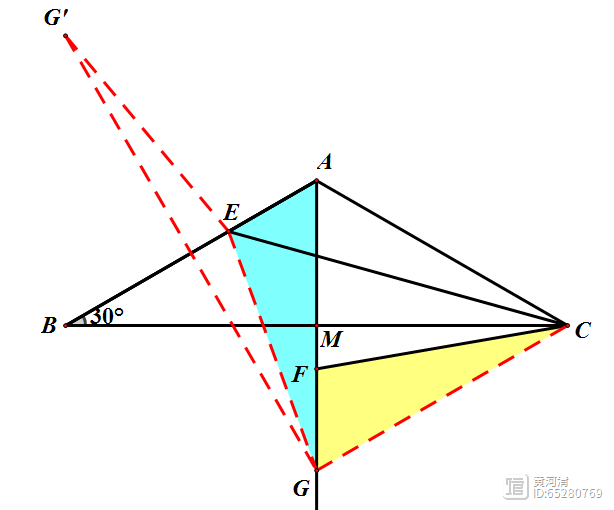
作G关于直线AB的对称点G'，则GE=G'E，当G'、E、C三点共线时，CE CF=CE GE=CE G'E取得最小值，等于G'C的长度

（3）利用等边三角形的性质进行计算

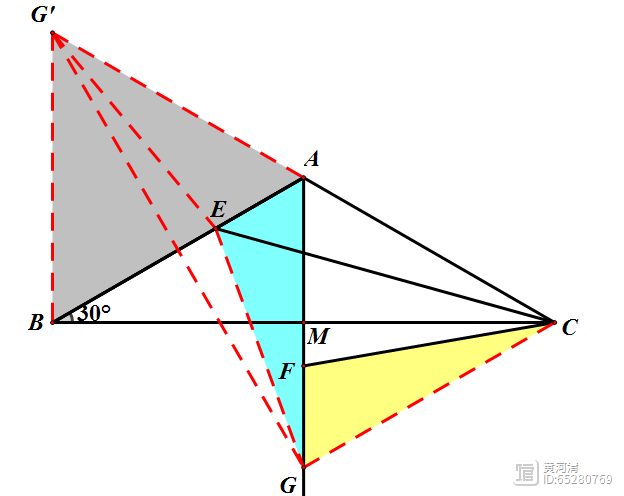
此时能发现△G'BA为等边三角形，从而G'、A、C三点共线。后续计算方法同上面逆等线的计算最后一步。

以上结束。