格点三角形中与求三角比、面积、相似三角形相关的问题


与求某个角的锐角三角比相关的问题
类型1:所求锐角在现成的直角三角形中,直接求解

解法分析:在第(1)题中,当图形中有现成的直角三角形时,可以直接借助图形中现成的直角三角形直接求解;在第(2)题中,根据旋转的意义,将角进行转化,从而求出tanB'的值。
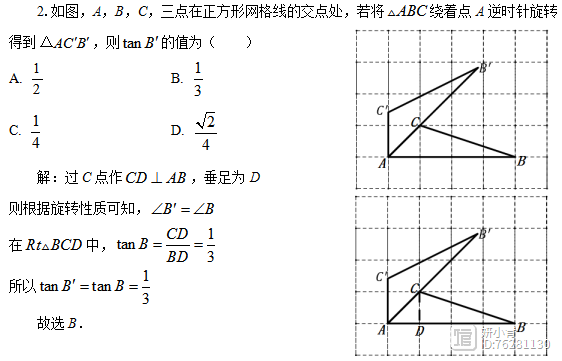

解法分析:在第(3)题中,由于△ABC的三边的长度是可求的,因此可以借助等积法求出AC边上的高求出cosA的值。
本题也可以通过利用∠C=45° ,求出BD的长度,求出cosA的值。



解法分析:在第(4)题中,本题的难点在于发现∠A=90°,若没有发现∠A=90°,则可以采取割补法,求出▲ABC的面积,再求BC边上的高,由于该三角形的三边均不平行(垂直)于正方形的各边,因此做两条高就显得过于复杂。

解法分析:在第(5)题中,由于∠AOC的位置比较“尴尬”,因此可以通过作平行线的方式进行转化。碰巧平移后的三角形是直角三角形,可以直接求解,若平移后的三角形是斜三角形,则采取“等积法”进一步求解。
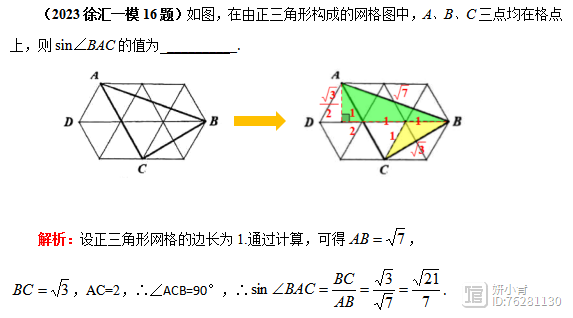
解法分析:和以往的正方形格点三角形不同,这次的格点三角形是由等边三角形组成的,比较新颖。利用60°角解三角形以及120°等腰三角形三边的比(1:1:
)可以求出三角形ABC各条边的边长,从而利用勾股定理逆定理得到△ABC为直角三角形。
求格点中的某个角的三角比,可以推广到平面直角坐标系中求某个角的三角形比,方法是相通的,要能够举一反三。


与三角形相似相关的问题
类型:根据相似三角形的判定定理画出所有符合题意的相似三角形
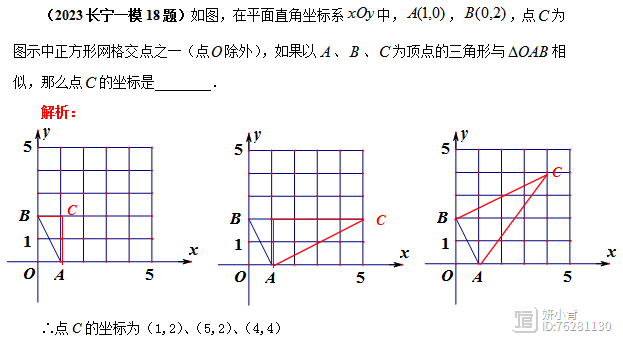
解法分析:本题的难点在于能否找全点C,因此可以利用相似比进行突破,即相似比分别为1、√2和2三种情况,画出符合题意的图形,从而求出点C的坐标。

解法分析:本题的背景是寻找与原三角形①有一个公共角;②各顶点在格点上的相似三角形。因此本题需要分类讨论,即平行型(A型)以及斜截型(斜A型),根据原三角形线段间的比例关系确定新三角形的具体位置。

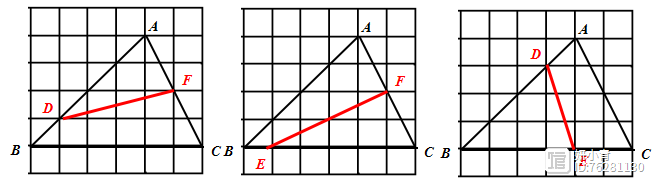


与三角形面积相关的问题
类型1:根据三角形之间的面积比画出符合题意的分割线
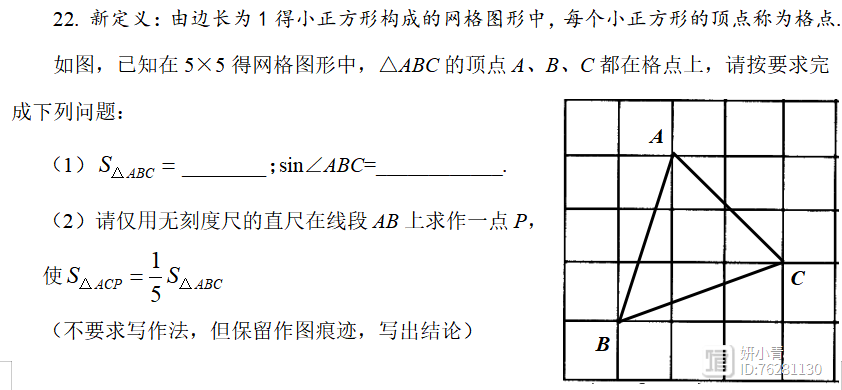
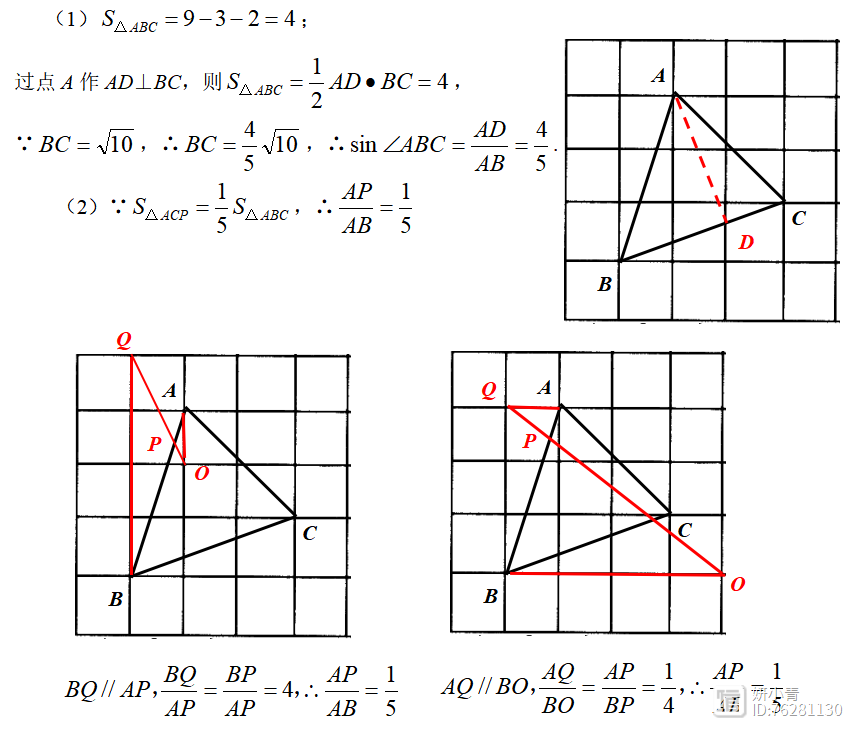
解法分析:本题的第(1)问是常规的格点三角形中三角形面积和锐角三角比的求法;第(2)问的灵活度就比较高了,根据面积比等于底之比,可得AB=5AP。但仅用一把无刻度的直尺如何作出一条的五等分点?依靠格点可以定位,再巧妙结合图中的X型基本图形确定P点位置,这种考察方式对于学生的综合素养和应变能力要求很高!
类型2:画出与原三角形相似的面积最大/最小的三角形
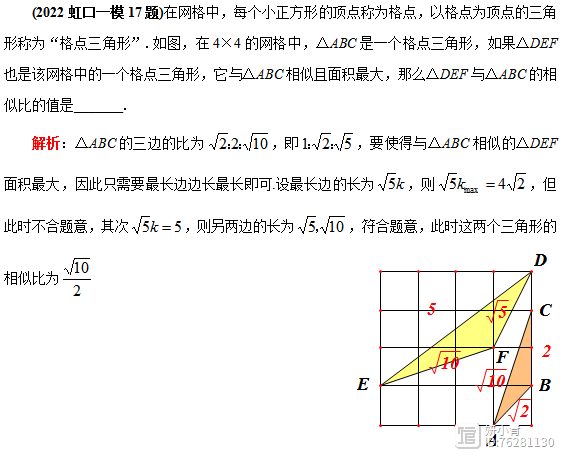
解法分析:本题的背景虽然是“格点三角形”,但是考察了相似三角形的相似比。本题的难点在于能够画出与△ABC相似且面积最大的三角形,通过分析目标△ABC的三边的比例关系从而找到△DEF三边的比例关系。



点个在看你最好看

- 0000
- 0000
- 0000
- 0000
- 0000