数学学习 | 高中知识点解析与讲解 - 平面向量基本定理!(值得学习)

之前我们学习了平面向量的概念、表示和相互关系等基础知识,还学习了平面向量的加减法、数乘和数量积运算,为了保证学习效果,同学们要及时回顾哦!
今天,我们就来学习一下平面向量基本定理相关的知识点,快看下去吧!

平面向量基本定理定义首先我们先来了解一下平面向量基本定理的概念:如果e1,e2是同一平面的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使a=λ1e1 λ2e2;上周我们学习了e是单位向量,那么同一平面内的两个不共线的单位向量e1和e2组合在一起就称为表示其所在平面内的所有向量的一个基底,用{e1,e2}表示。

平面向量基本定理证明在了解了平面向量基本定理之后,我们需要对其进行证明。
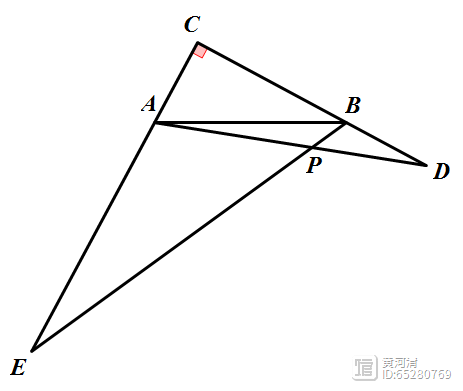
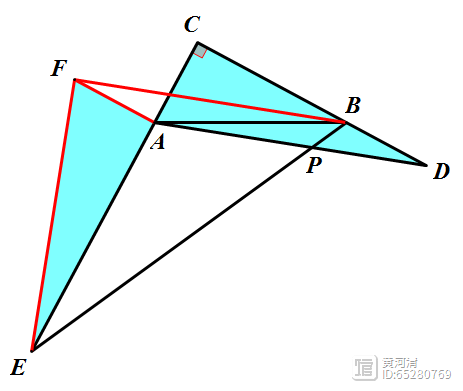
首先,在学习平面向量的加法运算的时候,我们学习了向量加法的三角形法则和向量加法的平行四边形法则,根据法则,我们知道一个向量可以表示为同一平面内两个向量的和,如:

又通过上周学习的向量数乘运算,我们可以得到位于同一直线上的向量可以由位于这条直线上的一个非零向量表示;
那么,针对上图,我们取与向量a共线的单位向量e1和实数λ1,则a=λ1e1,我们取与向量b共线的单位向量e2和实数λ2,则b=λ2e2,因此向量a b=λ1e1 λ2e2,我们便得到了部分平面向量基本定理;
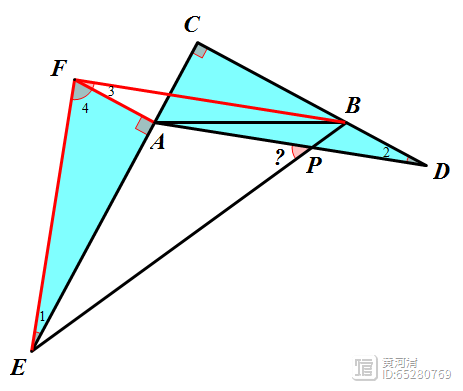
接下来我们证明定义中的“唯一性”:
假设存在μ1和μ2也可以表示向量a b为μ1e1 μ2e2,则λ1e1 λ2e2=μ1e1 μ2e2,即(λ1-μ1)e1 (λ2-μ2)e2=0,再假设λ1-μ1和λ2-μ2不全为零,则可以得到e1=[(λ2-μ2)/(λ1-μ1)]e2或e2=[(λ1-μ1)/(λ2-μ2)]e1,也就是说存在非零实数可以使单位向量e1和e2相互表示,也就是说单位向量e1和e2是共线的,这与已知的“e1,e2是同一平面的两个不共线向量”相矛盾;
因此,我们可以得到λ1=μ1,λ2=μ2,也就是说有且只有一对实数λ1和λ2满足向量a b=λ1e1 λ2e2。

平面向量的正交分解根据平面向量基本定理,我们了解到一个向量可以用两个同一平面的不共线的单位向量表示,如果这两个不共线的单位向量相互垂直,则称为将向量进行正交分解。
今天,我们学习了平面向量基本定理和正交分解,希望可以帮助同学们更好的进行高中数学学习哦!同学们有任何不懂的内容可以留言提问,如果有需要的话我们会有习题类推文哦!
TO BE CONTINUED ……
图片 | 网络(侵删)
- 0000
- 0000
- 0000
- 0000
- 0000