2023各区八年级25题解法分析

诺哈网2023-08-02 17:16:360阅

等腰三角形的存在性

对于八年级等腰三角形的存在性问题，需要分类讨论。首先是对等腰三角形的分类讨论，即AB=BC、AB=AC或BC=AC，排除不可能的情况。再次，是对点的位置的分类讨论，即点在线段上运动还是在射线上运动，根据题意画出图形后，利用图形中边、角的性质建立数量关系，从而求解。

压轴题解析

2023闵行八年级期末26题

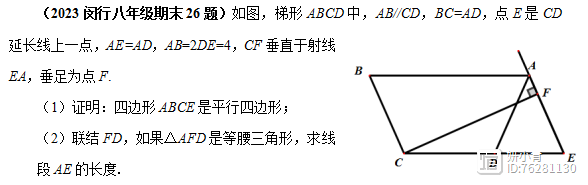
解法分析：本题的第(1)问是证明四边形ABCE是平行四边形，利用等腰梯形等腰三角形性质，得∠B=∠E，再利用AB//CD，得∠E ∠BCE=180°，从而得到BC//AB，继而得证。

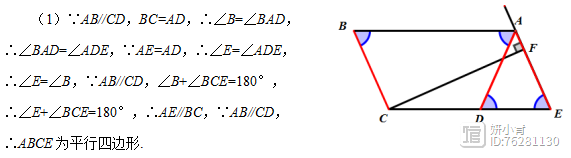
解法分析：本题的第(2)问是等腰三角形的存在性问题，需要分类讨论。首先对点F的位置分类讨论。当点F在线段AE上时，由于∠AFD>90°，此时有且仅有AF=DF这一种情况。通过条件可知D为Rt△CFE斜边上的中点，得到AF=DF=CD=BD=2，要求AE的长度，可以通过“等积法”求解。

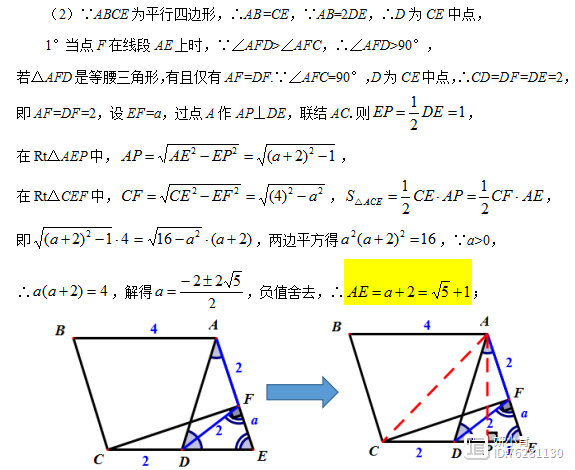
当点F在线段EA延长线上时，有三种情况，分别进行计算，排除不可能的请况。对于AF=AD，可得△CFE为等腰直角三角形；当AF=DF时，采取和情况1相同的解题策略；当AD=DF时，利用等腰三角形和三角形外角的性质排除不可能的请况。

2023静安八年级期末26题

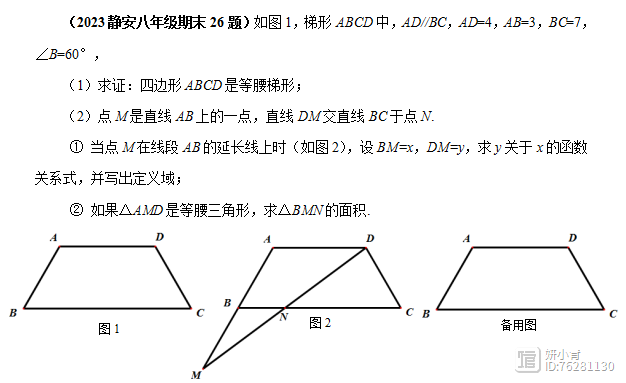
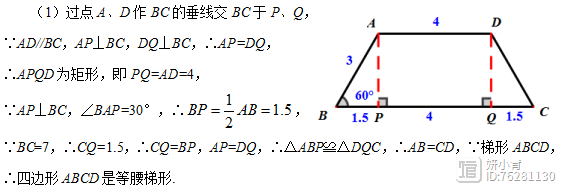
解法分析：本题的第(1)问是证明四边形ABCD是等腰梯形。由于已知了梯形部分边的长度以及∠B=60°，因此通过作两条高，通过求出CD的长度，从而确定AB=CD，继而得证。

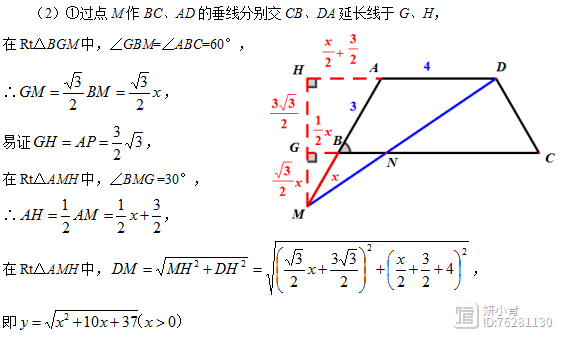
解法分析：本题的第(2)问的前提是动点M在直线AB上运动。第①问限定了M在线段AB上，如何建立函数关系成为了本题的难点，借助∠B=60°，通过过点M向CB、AD作垂线，利用勾股定理建立函数关系。

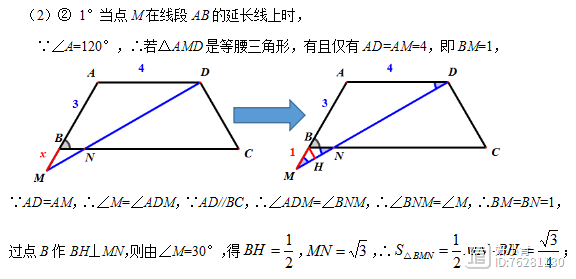
解法分析：第②问需要是等腰三角形△AMD的存在性问题，此时需要对点M的位置进行分类讨论。当点M在线段AB延长线上时，有且仅有AM=AD，此时可得BM=1，△MNB是顶角为120°的等腰三角形，通过过点B作MN的垂线，即可求出三角形面积。

当点M在线段AB上时，此时不存在。

当点M在线段AB反向延长线上时，此时点N和点C重合，△BMN此时为等边三角形，其边长为7。

2023普陀八年级期末25题

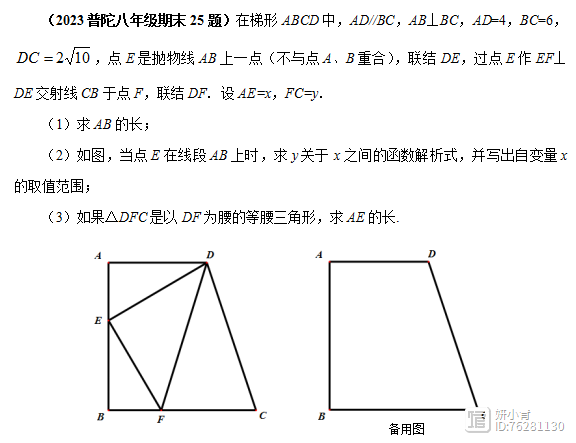
解法分析：本题的第(1)问通过过点D作BC的垂线，利用勾股定理，即可求得AB的长度。

解法分析：本题的第(2)问限定了点E在边AB上，建立函数关系，本题可以4次利用勾股定理建立函数关系。

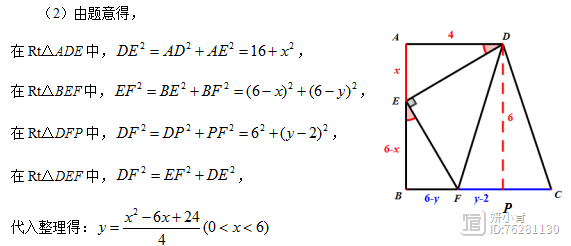
解法分析：本题的第(3)问是等腰三角形的存在性问题，需要分类讨论。即根据点E在线段AB或其延长线的两种情况进行分类讨论。

同类题链接

点击上方图片进行跳转

直角三角形的存在性

对于八年级直角三角形的存在性问题，需要分类讨论。首先是对直角三角形的分类讨论，即∠A=90°、∠B=90°，或∠C=90°，排除不可能的情况。再次，是对点的位置的分类讨论，即点在线段上运动还是在射线上运动，根据题意画出图形后，利用图形中边、角的性质建立数量关系，从而求解。

压轴题解析

2023长宁八年级期末25题

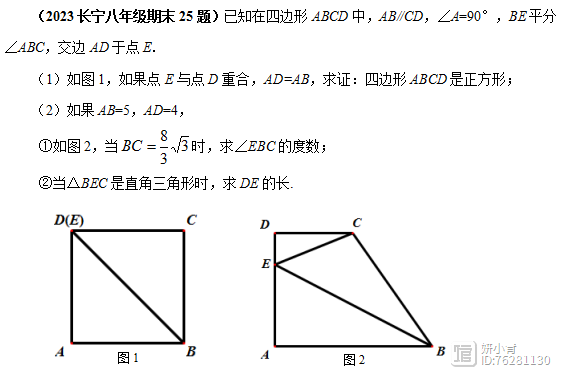
解法分析：本题的第(1)问是证明四边形ABCD是正方形，通过角平分线 AD=AB以及CD//AB，可得四边形ABCD为矩形，再利用“有一组邻边相等的矩形是正方形”进行判定。

解法分析：本题的第(2)问给定了AB和AD的长度。第①问是∠EBC的度数，通过过点C作AB的垂线，利用勾股定理解三角形，可得∠ABC=60°，继而得到∠EBC的度数。

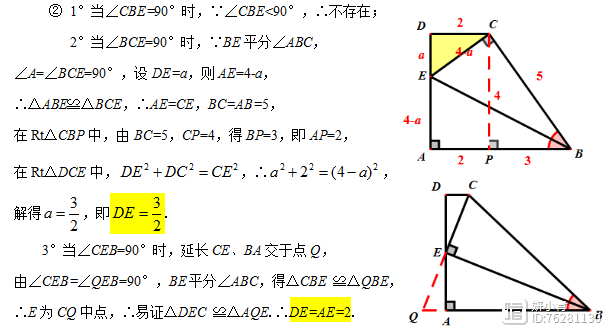
解法分析：第②问是直角三角形的存在性问题。当∠CBE=90°的情况首先排除；当∠BCE=90°时，可得△ABE和△BCE是全等的，继而再△DEC中利用勾股定理求出DE的长度；当∠CEB=90°，根据BE平分∠CBA，延长CE、AB交于点Q，构造等腰三角形，继而得到E为AD中点，从而得DE的长度。