小乐数学科普:给数学物理画上句号——译自AMS美国数学会专栏
宇宙中的基本力之一是弱力。弱力涉及将原子结合在一起或将它们分开......
作者:Ursula Whitcher(乌苏拉·惠彻) 2023-7-1
译者:zzllrr小乐,数学科普微信公众号 2023-7-4
你听说过句子末尾的句号(period)和正弦波的周期(period,该英文单词一词多义,译者注)。周期这个词在数论中也有特殊的含义。这些周期对于解决粒子物理学问题非常有用。在本月的专栏中,我将告诉你有关周期是什么、物理学的来历以及所有这些与甜甜圈几何形状的关系的更多信息。
从甜甜圈到积分
也许你听过这样一个笑话:拓扑学家无法区分咖啡杯和甜甜圈。(如果你不熟悉,请查看 Keenan Crane 和 Henry Segerman 绘制的有关两者变换的精美插图。)

几何学家能够区分咖啡杯和甜甜圈。我们甚至可以区分不同类型的甜甜圈。
例如,这是一个厚而甜的甜甜圈:

一个厚厚的饼状甜甜圈,上面覆盖着松软的糖
(照片由5th Luna拍摄, CC BY-NC 2.0)
这是一个薄脆的甜甜圈:

一个薄脆的甜甜圈,中间有个大孔
(照片由Janet Bianchini拍摄, CC BY-NC 2.0)
但甜甜圈的几何形状是如此令人着迷,一旦你开始检查它,就很难再考虑其他事情了!
让我们更正式地描述一下两个甜甜圈之间的区别。理想化的数学圆环曲面称为环面(torus,复数tori)。我们可以使用两个圆来表征圆环的形状,一个圆围绕外部,另一个圆穿过中心的孔。在一个厚厚的饼状环面上,这两个圆的大小大致相同。
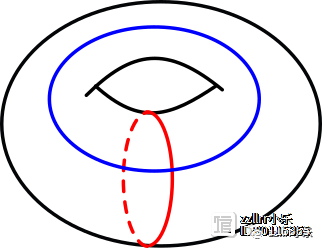
理想化数学的厚厚的甜甜圈,其圆围绕中心孔并通过中心孔。
在一个薄脆的圆环面上,外圆比内圆大得多。
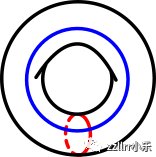
理想的数学的薄脆甜甜圈,大圆围绕中心孔,小圆穿过中心孔
在这些示例中,圆很容易测量。但有时环面以更复杂的方式出现。例如,假设x和y是复数变量,t是复数参数。考虑方程的解
y² = x(x-1)(x-t)
这就是著名的(对于数论学家来说)勒让德椭圆曲线(elliptic curve)族。如果我们在“无穷远”处引入一个解,那么从拓扑学上来说,它就是一个环面族。很难绘制两个复变量方程的解,但我们可以绘制实数值。当设参数t等于3 时,如下所示:
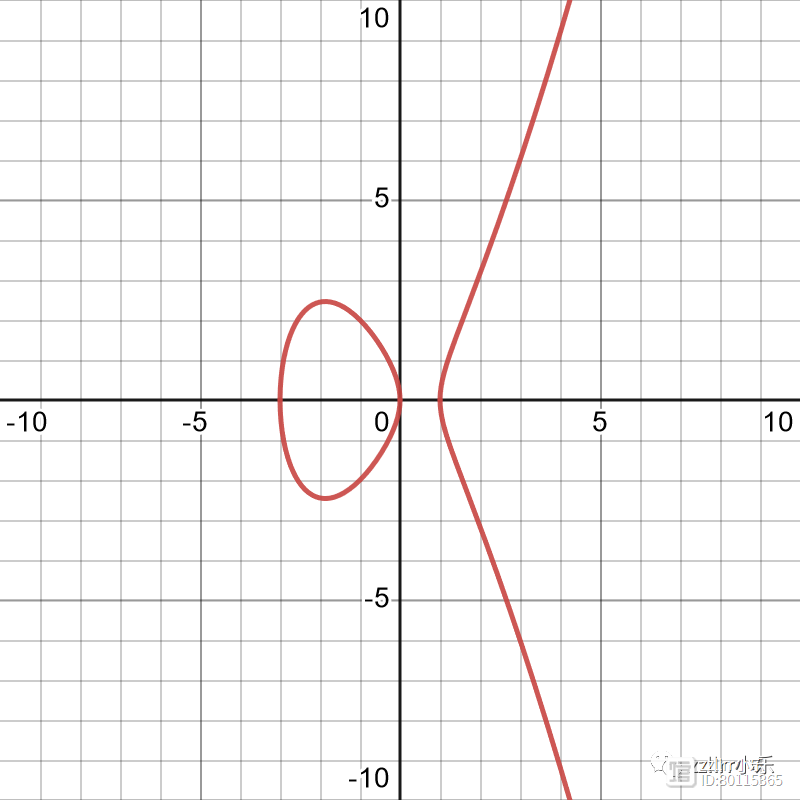
具有两个实数分量的椭圆曲线
你可以将绘制实数点的图形看作以一定角度切开甜甜圈。在此图中,你可以看到其中一个圆的倾斜版本和第二个圆的一部分。
测量这两个圆的长度很棘手。我们可以尝试微积分课上的一个通用数学策略:建立一个积分来测量弧长。在这种情况下,适当的积分是:
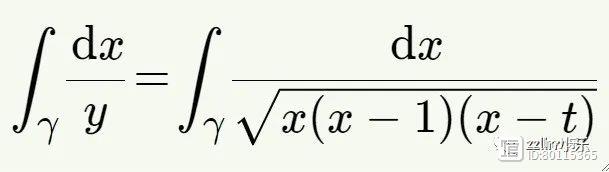
这里,积分是在环面/椭圆曲线中适当的简单闭合曲线γ上进行的。
但有一个问题!我将用一张容易混淆的橙色猫的漫画来解释它。

画了一只睁大眼睛的猫,它说哇,这个积分真的很难!
猫没有说谎:这个积分真的很难。微积分课上的标准技术不起作用。事实上,这个积分没有封闭形式的代数解。
周期和微分方程
积分
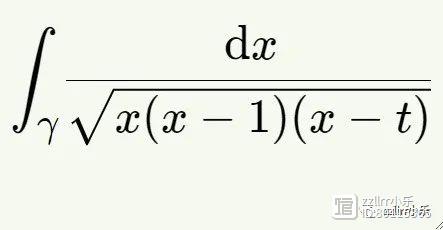
是一个周期的示例。对于数论学家来说,周期是一个通过在适当的子空间上求代数表达式的积分而得到的数字。(从技术上讲,我们应该能够使用不等式和有理系数的代数方程组来描述我们正在积分的区域。)
许多有趣的常量,例如 π 和 ㏒ 2,都可以写成周期。关于周期有很多大而有趣的问题:例如,我们如何描述哪些数字作为周期出现?使用积分运算,可以证明周期相加或相乘会产生一个新周期。这使得周期具有环(ring)的结构。另一个悬而未决的大问题是描述周期环满足的所有关系。
让我们回过头来尝试理解我们的特定周期。我们知道积分的结果是一个取决于参数t的数字,因此我们将积分视为函数P(t)。我们可以对其求导数:
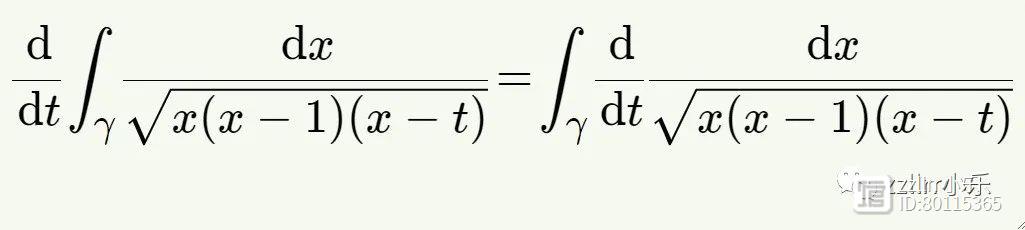
当我们求导时,积分符号下的表达式变得更加复杂,但它保持相同的一般形状。通过找到一个公分母(common denominator),我们可以确定P(t)、P'(t)和P''(t)之间的关系:
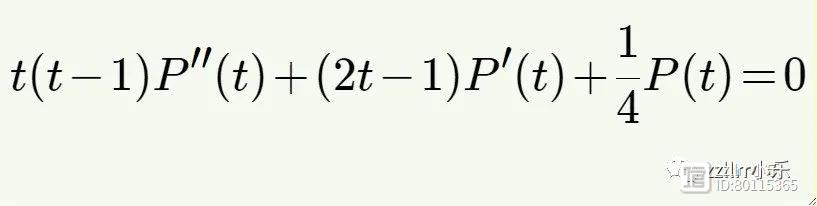
这是一个微分方程!(它被称为Picard-Fuchs 方程,以法国数学家 Émile Picard(埃米尔·皮卡) 和德国犹太数学家 Lazarus Fuchs(拉扎鲁斯·富克斯) 的名字命名。)作为二阶微分方程,该 Picard-Fuchs 方程有两个独立的解。这些解对应于环面上的两个不同的圆。
求解微分方程的标准方法是使用无穷级数(infinite series)。在这种情况下,我们周期的微分方程的解之一可以写成以下级数:
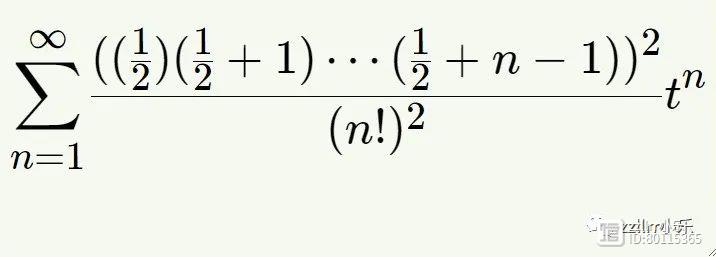
其中分子涉及一个表达式
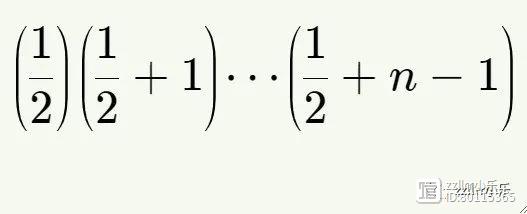
看起来很像上升阶乘移动了1/2一样。如果我们用简写
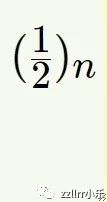
替换这个表达式,我们的级数就会得到更紧凑的表示法:
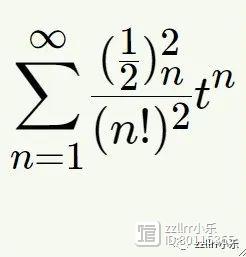
这是一个著名的级数,称为超几何级数(hypergeometric series),其分子参数为1/2,1/2;分母参数为1 (因为分母中只有一个阶乘)。整个级数有时用更紧凑的符号表达:
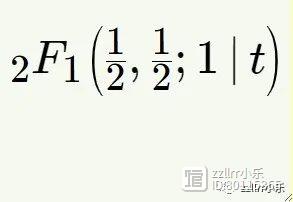
有关求解过程的更多详细信息,包括第二个独立周期的描述,请参阅 Don Zagier 的深入论文《微分方程的算术和拓扑》 /zagier/files/doi/10.4171/176-1/33/HirzebruchLectureECM2016.pdf 。我想向你展示理论物理学中出现的一个更复杂的周期。
日落和费曼图
在粒子物理学中,描述电子和光子等基本粒子之间的相互作用涉及计算困难的积分。(更糟糕的是,从数学家的角度来看,这些积分可能并不总是良好定义的!)物理学家使用复杂性不断增加的称为费曼图(Feynman diagrams)的图表来组织这些计算。创建和操作费曼图有特定的规则,但在初步近似时,人们可以想象它们讲述了粒子相遇、相互作用并可能经历转变,然后分道扬镳的故事。
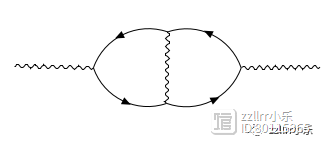
具有多个循环的费曼图
宇宙中的基本力之一是弱力(weak force)。弱力涉及将原子结合在一起或将它们分开。它是控制放射性衰变过程并使碳14检测年龄成为可能的力量。

一棵树的横截面
人们可以利用树木年轮来校准碳-14测年的方法。比尔·卡斯曼拍摄(公共领域)。
要进行涉及弱力的计算,必须使用包含循环的费曼图。这是一个带有两个循环的费曼图,有时称为日落图(sunset diagram)。
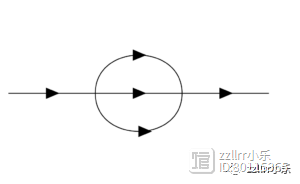
看起来像穿过圆心的箭头的费曼图
美国数学家斯宾塞·布洛赫(Spencer Bloch)和法国物理学家皮埃尔·范霍夫(Pierre Vanhove)联手研究日落图。为了简化问题,他们使用了一个只有两个时空维度的模型。(想象粒子随着时间的推移沿着一条线来回移动。)他们假设相互作用过程中产生的所有粒子都具有相同的质量m,有一个固定的外部动量K,并且他们输入了一个常数μ来平衡单位。结果是以下日落积分:
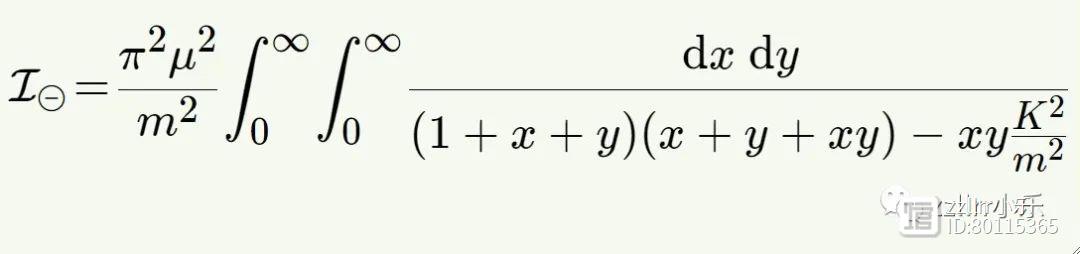
这个积分真的非常非常难!
关键问题之一是其分母可能为 0。要了解更多关于哪里分母消失,我们可以设
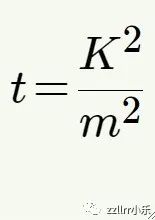
结果是一个取决于参数 t的曲线族:
(1 x y)(x y xy) - txy = 0
这是 t=11 的结果图。
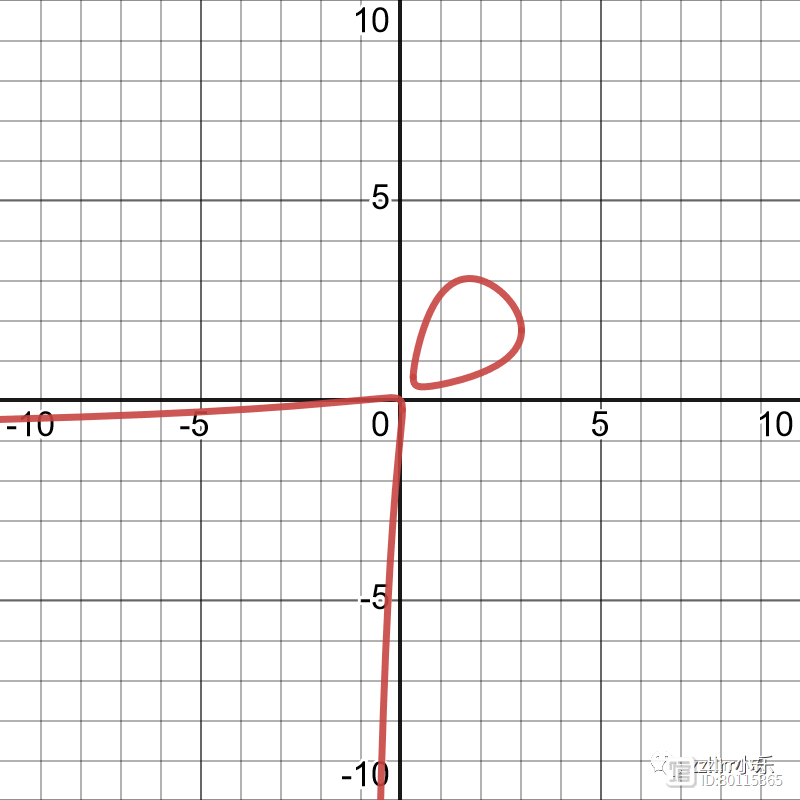
具有两个实数分量且关于直线 y=x 对称的椭圆曲线
该图的特征可能看起来很熟悉。我们有一个倾斜的圆和另一个圆的一部分——甜甜圈切片又回来了!换句话说,(1 x y)(x y xy) - txy =0 是参数化的椭圆曲线族。
布洛赫和范霍夫采取了一种看似熟悉的策略。他们设
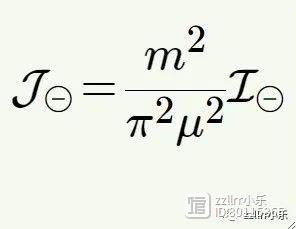
来简化单位,然后寻找一个涉及J的微分方程,
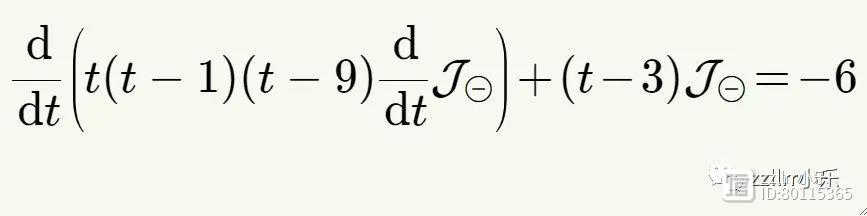
由于该微分方程的右侧不为零,因此求解它比求解我们之前看到的微分方程更复杂。标准微分方程方法分两步解决此类问题。首先,求解齐次方程(homogeneous equation),假设右侧为零。然后,找到非齐次方程(inhomogeneous equation)的解,其中右侧是非零常数。
布洛赫和范霍夫证明,关于J⊝的Picard-Fuchs 微分方程的齐次解可以用经典超几何级数来写:

这个级数用涉及 1/12和5/12的上升阶乘替换我们之前看到的 1/2。我使用 − 来指示为级数变量插入了更复杂的表达式。
为了求解完整的非齐次方程,我们需要另一个特殊常数Li₂(z),称为二重对数(dilogarithm)。二重对数可以写成无穷级数。当|z| < 1时,
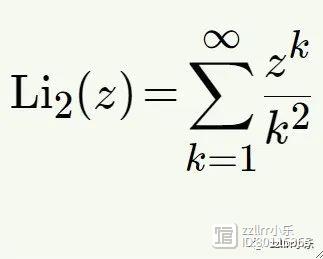
二重对数也是一个周期!我们可以用二重积分来写它。
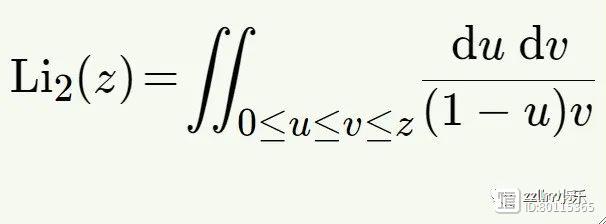
因此,周期为我们提供了一种精确的方法来描述日落图积分的解,同时也是吃甜甜圈的理由!
进一步阅读
Spencer Bloch 和 Pierre Vanhove,日落图的椭圆二重对数。J. Number Theory 148 (2015), 328–364. MR3283183, arXiv:1309.5865 [hep-th]。
马克西姆·康采维奇和唐·扎吉尔,周期。Mathematics unlimited—2001 and beyond, 771–808, Springer, Berlin, 2001. MR1852188, IHEP
Stefan Müller-Stach, 什么是……周期?AMS 通知, 2014年9月
Don Zagier,微分方程的算术和拓扑。欧洲数学大会,717–776, Eur. Math. Soc., Zürich, 2018. MR3890449, MPIM
唐·扎吉尔 (Don Zagier),《非凡的二重对数》。J. Math. Phys. Sci. 22 (1988), no. 1, 131–145. MR940391, MPIM
致谢
我感谢英国剑桥艾萨克·牛顿数学科学研究所在 K 理论、代数环和动机同伦理论项目期间给予的支持和热情接待,我在该研究所的 30周年庆祝活动期间展示了该内容的一个版本。这项工作得到了 EPSRC (编号EP/R014604/1)的支持。
参考资料
/featurecolumn/2023/07/01/period-math-physicals/
小乐数学科普:帽子戏法——美国数学会科普专栏
小乐数学科普:一种不一样的距离感——Maria Fox美国数学会专栏
小乐数学科普:矩阵是什么?——James Propp教授专栏
小乐数学科普:预测友谊和其他有趣的图机器学习任务——译自AMS美国数学会专栏
让数学
更加
易学易练,
易教易研,
易赏易玩,
易见易得,
易传易及。
- 0000
- 0009
- 0000
- 0009
- 0000











