一题多解 | 特殊角辅助线构造方法
诺哈网2023-08-20 08:54:290阅
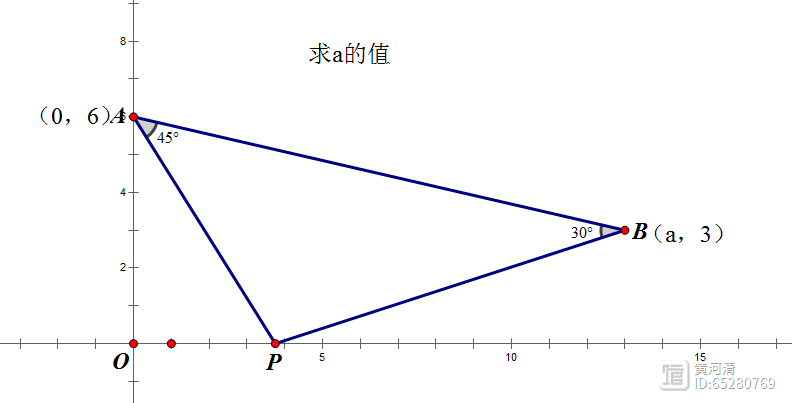
如下图所示,A(0,6),B(a,3)且a>0,P在x轴上,其中∠PAB=45°,∠PBA=30°,求a的值。
解法1:看到45°,30°特殊角,直接构造垂线

①PC⊥AB,得到两个特殊角三角形
②构造一线三垂直全等,得到△AEC≅△CDP
③构造一线三垂直相似,得到△BFC∼△CDP
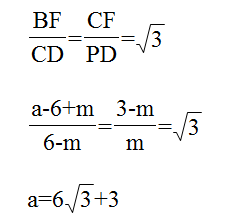
④计算求出m的值、a的值(计算的时候注意整体思想)
解法2:以45°构造等腰直角三角形
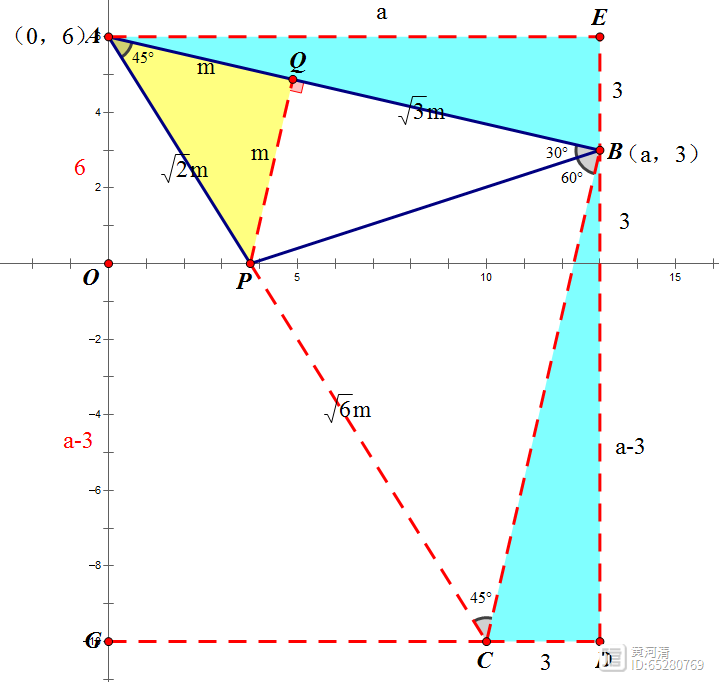
①构造等腰直角三角形ABC
②构造一线三垂直全等,△AEB≅△BDC
③解△ABP,得到AQ:QB=1:√3,从而得到AP:PC=1:√3
④△AOP∼△AGC,求得a的值;
解法3:四点共圆+相似

①特殊角构造直角三角形,PD⊥AB
②A、O、P、D四点共圆,同弦所对的圆周角相等,所以∠DOP=∠DAP=45°;
③构造等腰直角△OEF;
④△ADO∼△BDE
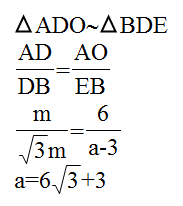
⑤从而求出a的值;
解法4:三点共圆的的巧妙运用
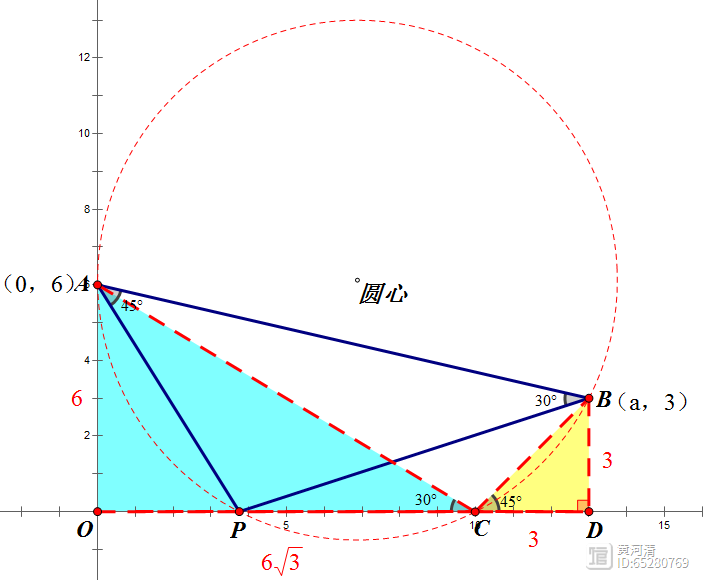
①以A、P、B三点构圆
②结合上图,A、P、C、B四点共圆;所以:
∠ABP=∠ACP=30°;(同弧所对圆周角相等)
∠BCD=∠PAB=45°;(对角互补、邻补角互补)
③解三角形,很容易算出OC=√3AO=6√3;CD=BD=3;
④所以a=6√3 3
0000
评论列表
共(0)条相关推荐
- 0000
- 0000
- 0000
- 0000
- 0000