圆锥曲线三角形面积与四边形面积题型全归类
诺哈网2023-08-16 11:27:310阅
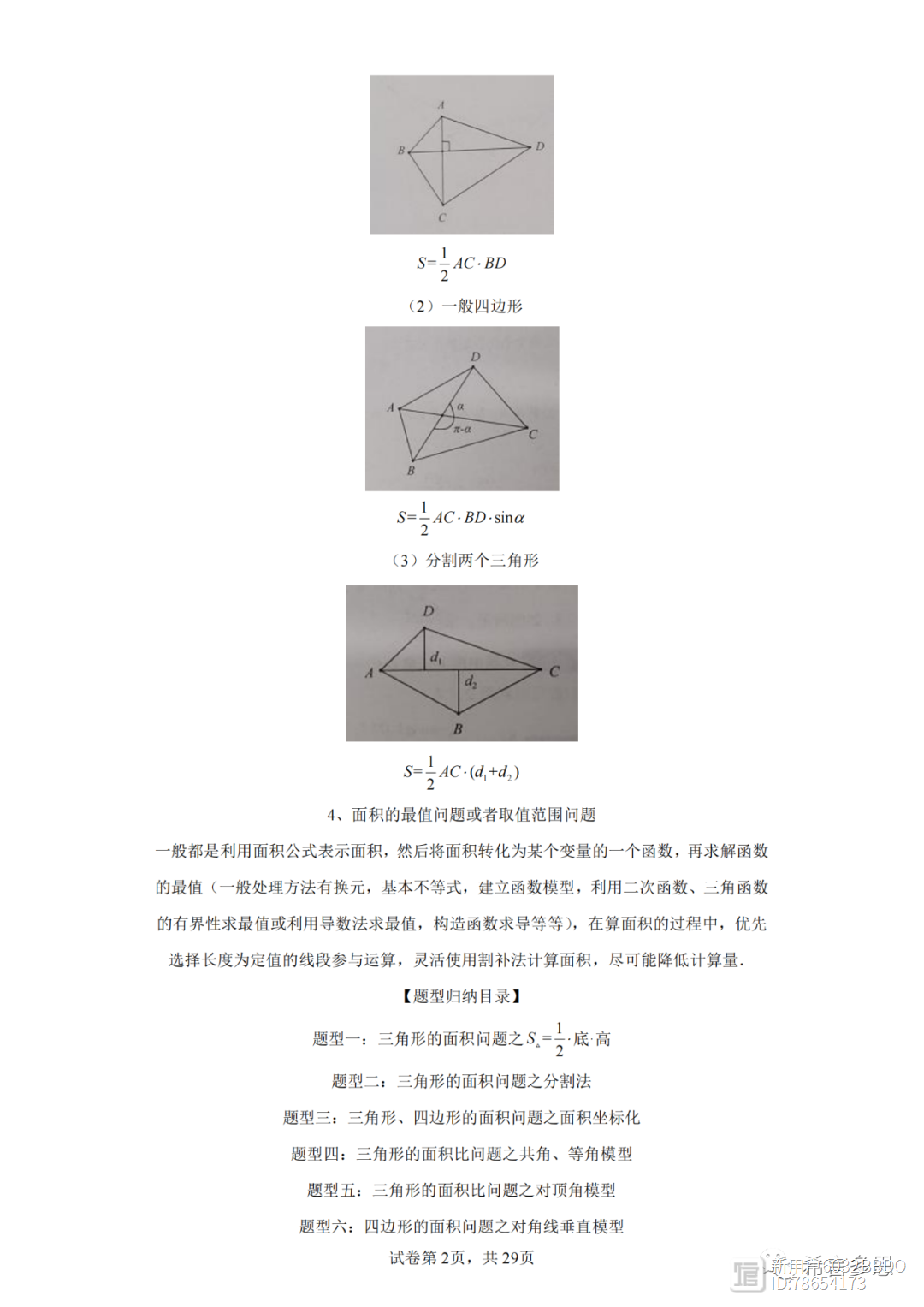


































































4、面积的最值问题或者取值范围问题
一般都是利用面积公式表示面积,然后将面积转化为某个变量的一个函数,再求解函数的最值(一般处理方法有换元,基本不等式,建立函数模型,利用二次函数、三角函数的有界性求最值或利用导数法求最值,构造函数求导等等),在算面积的过程中,优先选择长度为定值的线段参与运算,灵活使用割补法计算面积,尽可能降低计算量.
【题型归纳目录】
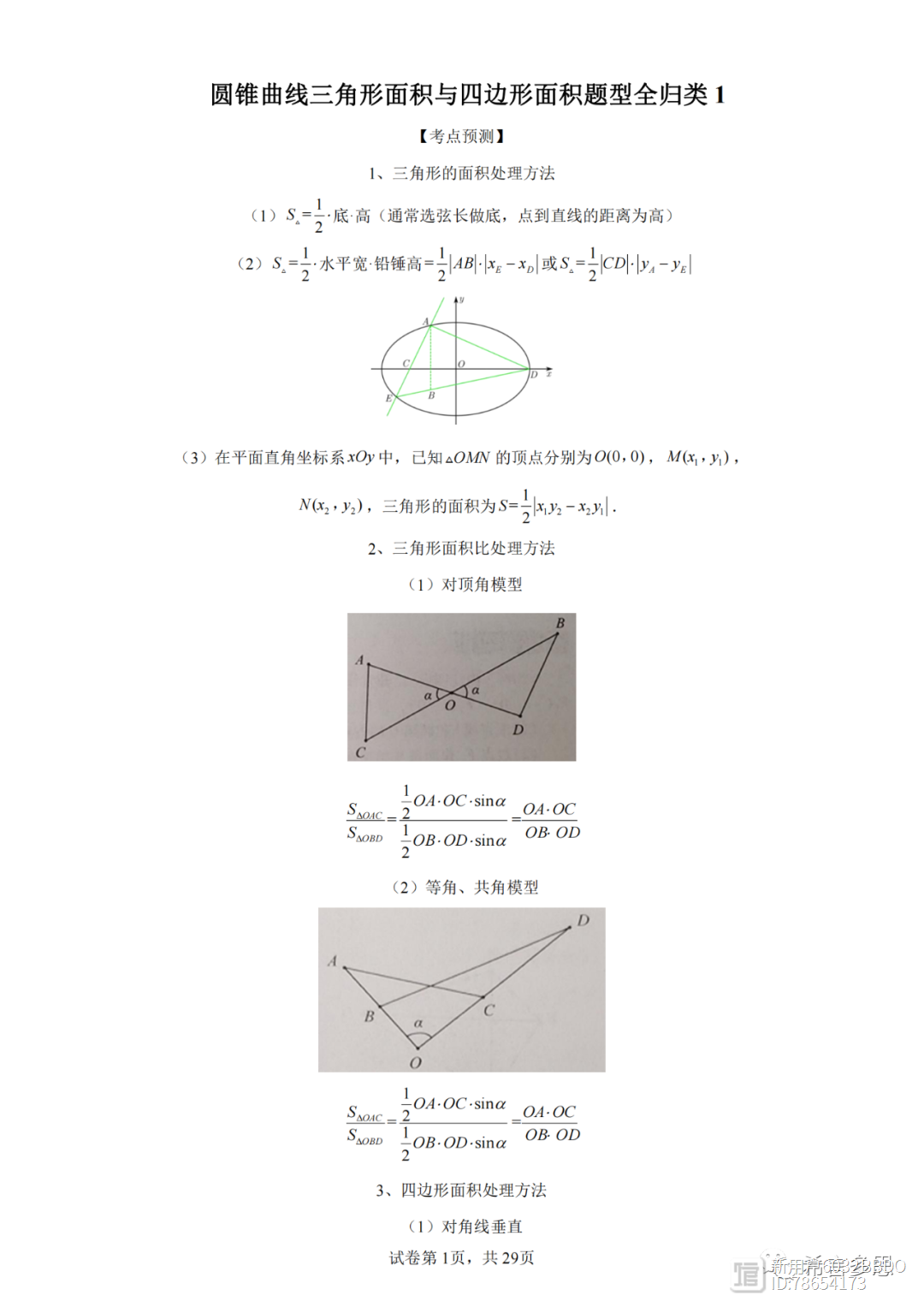
题型一:三角形的面积问题之底·高
题型二:三角形的面积问题之分割法
题型三:三角形、四边形的面积问题之面积坐标化
题型四:三角形的面积比问题之共角、等角模型
题型五:三角形的面积比问题之对顶角模型
题型六:四边形的面积问题之对角线垂直模型
题型七:四边形的面积问题之一般四边形
【典例例题】
题型一:三角形的面积问题之底·高
(2022·上海市复兴高级中学高三开学考试)
1.已知椭圆的离心率为,其左焦点到点的距离为.
(1)求椭圆的方程;
(2)直线与椭圆相交于两点,求的面积关于的函数关系式,并求面积最大时直线的方程.
【答案】(1)
(2),,直线的方程为.
【分析】(1)利用题干条件列出方程,求出,进而计算出,写出椭圆方程;
(2)联立直线与椭圆方程,得到两根之和,两根之积,利用韦达定理求出弦长,进而求出点到直线距离,表达出面积,并用导函数求解最大值及面积取得最大值时直线的方程.
0000
评论列表
共(0)条相关推荐
- 0000
- 0000
- 0000
- 0000
- 0000