正方形中的简易探究,折叠探路,最值结尾
诺哈网2023-08-14 11:26:490阅
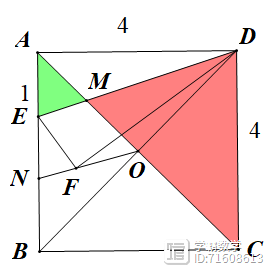
如图1,已知正方形ABCD的边长为3,E为AB上一点,把△ADE沿直线DE对折后,点A落在点F处
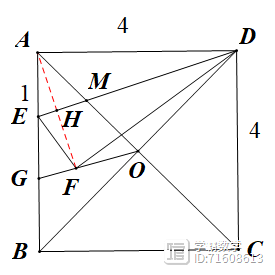
(1)当AE=1时,如图2,正方形的对角线AC与DE相交于点M,与正方形另一条对角线BD相交于点O,连接OF并延长交AB于点G
①求
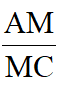
的值,并说明点M是OA的中点;②试探究OG与DE有怎样的位置关系,并说明理由;③求线段GF的长;
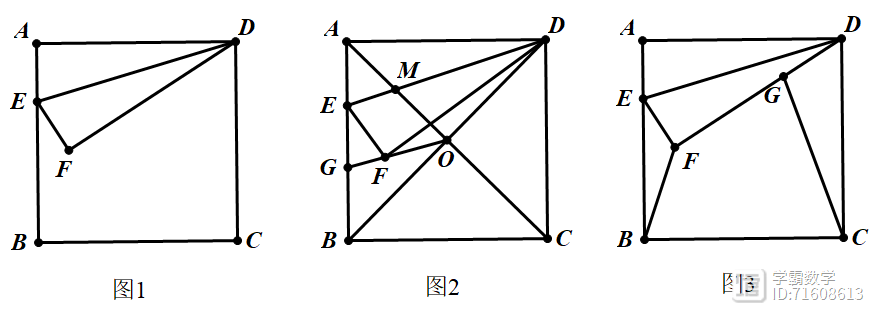
(2)如图3,点G是线段DF上的一点,且DG=1,连接BF、CG,则在点E从点A运动到点B的过程中,BF CG的最小值为_________,此时BF的长为_________.
解:(1)
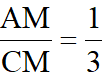
,由AE||CD易知
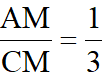
,即有

,得OA=2OM,故M为OA的中点;
OG||DE,连接AF交DE于点H,易知AF⊥DE且H为AF的中点,而M为OA的中点,故HM||OF,即有OG||DE;
在ADE中,由射影定理可知EH·ED=EA2,得EH=

得GF=

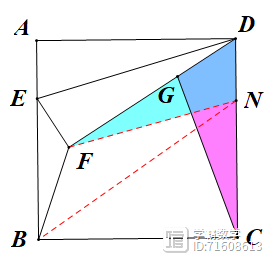
(2) 在CD上取一点N,使DN=DG=1,易知△DFN△≌DGC,GC=FN,BF CG=BF NF,当B、F、N共线时,取最小值,最小值为
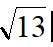
点评:题目整体难度不大,第一问中的辅助线会比较关键;而第二问的线段最值,则主要考虑构造全等转化线段.
关于学霸数学
"学霸数学"专注于数学中考高考考试的最新信息,好题与压轴题解题技巧、知识专题分析以及考试分析与解答,考试动向及政策分析解读、家庭教育相关分享!如果您是家长或学生,对学习方面有任何问题,请联系小编!
0000
评论列表
共(0)条相关推荐
- 0000
- 0000
- 0000
- 0000
- 0000








