浙江高考英语“七选五”，我是这样得满分的。

今年冬天特别冷，寒潮接二连三地，让西湖都冻了冰。然而，让浙江考生冻得瑟瑟发抖的，不是西湖的冰，也不是卡住头的南瓜，而是2021年1月的英语试题中的“七选五”。

学生1：阅读还行，七选五开始难了。

学生2：七选五难，完形难，语法也难。

学生3：七选五我真的很想骂人花了至少十几分钟在这上面，以至于完形很赶赶在五分钟写完

学生4：但是从七选五开始，出卷人可能想展示一下“浙江精神”，七选五，难，有点绕

学生5：七选五太慢了，时间都用完了。

学生6：七选五看不懂啊

学生7：七选五真的纠结

学生8：七选五是个啥

好吧，现在是凌哥套着南瓜做七选五的时刻了！

第二节（共 5 小题；每小题 2分，满分 10 分）

根据短文内容，从短文后的选项中选出能填入空白处的最佳选项。选项中有两项为多余选项。

[1] You run into the grocery store to pick up one bottle of water. You get what you need, head to the front, and choose the line that looks fastest.

[2] You chose wrong. People who you swear got in other lines long after you are already checked out and off to the parking lot. (31)______

[3] It turns out, it's just math working against you; chances are, the other line really is faster.

[4] Grocery stores try to have enough employees at checkout to get all their customers through with minimum delay. (32)______ Any small interruption --- a price check, a chatty customer --- can have downstream effects, holding up an entire line.

[5] If there are three lines in the store, delays will happen randomly at different registers. Think about the probability: (33)______ So it's not just in your mind: Another line probably is moving faster.

[6] Researchers have a good way to deal with this problem. Make all customers stand in one long, snaking line --- called a serpentine line --- and serve each person at the front with the next available register. (34)______ This is what they do at most banks and fast-food restaurants. With a serpentine line, a long delay at one register won't unfairly punish the people who lined up behind it. Instead, it will slow down everyone a little bit but speed up checkout overall.

[7] (35)______ It takes many registers to keep one line moving quickly, and some stores can't afford the space or manpower. So wherever your next wait may be: Good luck.

A. Why does this always seem to happen to you?

B. So why don't most places encourage serpentine lines?

C. Some of them may have stood in a queue for almost an hour.

D. The chances of your line being the fastest are only one in three.

E. How high is the probability that you are in the fastest waiting line?

F. With three registers, this method is much faster than the traditional approach.

G. But sometimes, as on a Sunday afternoon, the system gets particularly busy.

亲，您也可以先自己尝试做一做呀。

报告！凌哥一次性做对啦！所以很荣幸地和大家分享一下自己的思考过程。尤其请注意大红的文字哦，就是传说中的答题秘笈！

一、如何处（bi）理（kai）陌生词汇？

有一些考生反映说陌生词汇影响了做题。凌哥看了一下，这篇文章中可能的陌生词汇（对于学生来说，学过的词汇也可能变成陌生词汇啦）有：grocery, swear, minimum, interruption, chatty, downstream, randomly, register, serpentine, manpower。

1. grocery：出现于grocery store。能知道store的含义就可以了。或者能读懂这篇文章是在讲“排队”就可以了。

2. swear：这里要能根据动词来解构嵌套语句People (who (you swear) got in other lines long after you) are already checked out and off to the parking lot.这样解构之后，“you swear”就可以直接删除了。

3. minimum：出现于with minimum delay。如果根据日常生活经验，知道商家要尽快让顾客们完成结账，就会知道with minimum delay相当于without delay。

4. interruption、chatty、downstream：出现于语句Any small interruption --- a price check, a chatty customer --- can have downstream effects, holding up an entire line. 其实能根据句子理解A price check or a customer can hold up an entire line.就可以了，因为生词并不影响前后语句的逻辑关系。

5. randomly、registers：出现于If there are three lines in the store, delays will happen randomly at different registers. Think about the probability: (33)______ So it's not just in your mind: Another line probably is moving faster. 为什么凌哥将整一段复制到这里了呢？因为有2个重要的同源词：probability / probably.这2个词能够很好地印证randomly的含义。顺便说一下：probability其实是一个数学术语：概率。而猜测registers的含义则要容易得多，尽管——更标准的说法是cash registers（收款机）。

6. serpentine：出现于in one long, snaking line --- called a serpentine line。显而易见，无需解释。

7. manpower：出现于It takes many registers to keep one line moving quickly, and some stores can't afford the space or manpower. manpower是复合词，拆开来就知道意思了。

这样的陌生词汇分析过程有助于简化语篇的含义。

二、词汇对于确定选项有什么帮助？

梳理选项中陌生词汇出现的顺序很重要。请看选项B中的serpentine和选项F中的registers，分别出现在第[6]段和第[5]段。结合语义来判断，选项B不可能用于[1 - 5]段，选项F不可能用于[1 - 4]段。

三、如何明确逻辑关系？

先告诉您答案：AGDFB

先要明白很多此类型的外刊文章的行文套路：先给出一个实例（通常以一个人，或一个虚拟的you，为主人公）来引出现象和问题——“抑”，本文中是[1 - 2]段。然后再讲述导致问题的原因，并分析可能的对策，本文中是[3 - 5]段。最后再为这个主人公提建议——“扬”，可是很不幸的是，在该语篇中，这个问题是难以解决的，所以给的建议是“听天由命”。

所以，第31小题还是处在实例描述阶段，说的是一个让人郁闷的排队问题：明明自己选的是“看起来最快的队伍”，结果却是别的队伍捷足先登。所以选项A就强化了这个现实问题。

第32小题主要看前后三个句子的逻辑关系：选项句是对前一句的转折，最后一句是对选项句的具体化。这样就确定了答案G

第33题难倒凌哥了！！整一段都是在讲“概率”的。作者假设了三个队伍的概率。凌哥一开始觉得选项D和选项E表达的是同一个意思，只不过一个用了陈述句，另一个用了诘问句。所以，做题的时候，先将两个选项D/E都填了进去，——这样就不会给做其他题目的时候造成干扰了。

最后凌哥是怎么解决这个小题的呢？再仔细辨读上下文，通过前一句“Think about the probability:”来判断后面需要一个陈述句。最终确定答案是D。

第34题，前面已经说到，通过词汇registers可以判断选项F之后用于第33-35小题。前面AGDE已经用掉或者去掉了，所以先将F放进去读一读。嗯，味道不错。然后再将B和C放进去比较一下，完全意思不通啊！做这一题的成功率，依赖于“通过前面几题缩小了选项范围”，当然，也还可以通过下文来更好地验证。

前面说了这类文章的行文特点，那么第[7]段就不应该是解决方案和建议吗？然而，从最后一句可以看出，作者并没有给出切实的解决方案，而是“Good luck（全看运气了）”，由此可以判断前面的serpentine line并没有被使用起来，所以确认了答案是B。再说了，选项C放在这里已经完全不通顺了。

这一段中，除了第35题选项句，都是命题者改写的语句。但是凌哥个人认为，如果“and some stores ...”改成“but some stores ...”，题目就简单多了。这样一改之后，该句与选项B的逻辑关系会更加清晰。那么，“and”错了吗？并没有错。因为这个句子陈述了不能实现蛇形队伍的3个困难：得需要很多收款机（many registers），更何况（and）有些店负担不起空间和人力（space and manpower）。

这里还有一个问题就是选项中的“so”的用法。设想一下，如果改成“However, why don’t most places encourage serpentine lines?”，是不是更加符合我们汉语的思维呢？——可是，如果我们接触了网络流行语的话，就明白了：“那么问题来了，……”，而不是说“可是，问题来了，……”。所以，这个“So”放在问句中的时候，并非表示“总结”，而是表示“引发一个问题”，相当于“then arises a question”。看，Collins词典是这么说的：

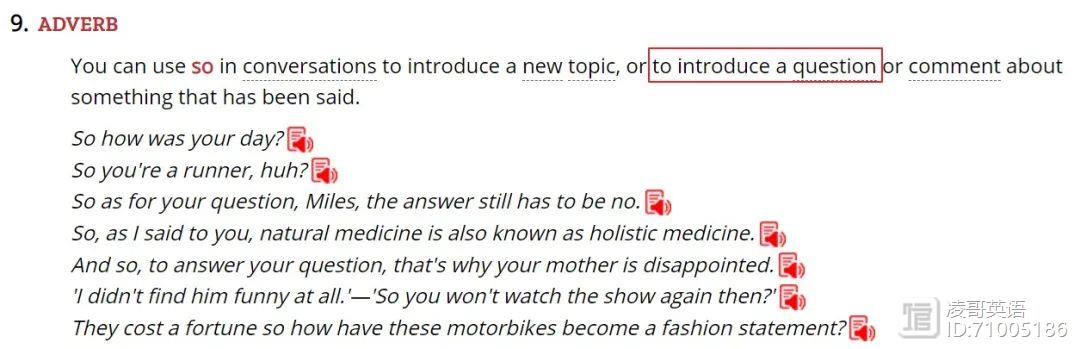
从第[7]段看，虚词往往体现了逻辑关系，多了解一些虚词的特别含义，对于“七选五”的解题是大有好处的。

试题来源，看过来！

/2014/07/whats-up-with-the-other-line-is-always-faster/

YOU RUN INTO the grocery store to quickly pick up one ingredient. You grab what you need and head to the front of the store. After quickly sizing up the check-out lines, you choose the one that looks fastest.

You chose wrong. People you could swear got in other lines long after you chose yours are already checked out and headed to the parking lot. Why does this seem to always happen to you? What kind of a cruel universe would allow such a thing to happen? It's not fair!

Well, as it turns out, it's just math that is working against you.

When you’re selecting among several lines at the grocery store, the odds are not in your favor. Chances are, the other line really is faster. Mathematicians who study the behavior of lines are called queueing theorists, and they’ve got the numbers to prove this. Their models also underlie a diverse set of modern problems, including traffic engineering, factory design, and internet infrastructure. At the same time, queueing theory provides a fairer way to checkout at the store. The only problem is that many customers don’t like it.

Before we get into that, we need to start at a somewhat unexpected place: the Copenhagen telephone exchange. In the early 1900s a young engineer named Agner Krarup Erlang was trying to figure out the optimal number of phone lines for the city’s switchboard. This is back in the day when operators were actual physical human beings and they connected telephone calls by plugging a jack into a circuit.

To save on labor and infrastructure, Erlang wanted to know the minimum number of lines that would be necessary to make sure that pretty much everyone’s calls could get connected. For a really cheap switchboard, you could have just one line. But then making a call would be a horrendous ordeal for customers, who would have to wait behind anyone else trying to talk at the same time. And having a line for each of the city’s thousands of telephones also doesn’t make practical sense.

Let’s look at a simplified example. If the Copenhagen switchboard has to deal with an average of two phone calls per hour, you might expect that two lines could suffice. But this fails to take into account the fact that there will be some hours when there are more calls, and some hours with less. During a very busy time, the switchboard might receive five requests for connections. With two lines, it can only provide calls for two customers, putting the rest on hold. If the Danes are particularly chatty, these calls could last an hour, meaning that more calls will arrive in the meantime, and the entire system will quickly back up.

Erlang devised equations that took into account the average number of phone calls in a given hour and the average amount of time for each call. Using his calculations in the simple example above, the Copenhagen telephone exchange would find out that they need seven lines to make sure that 99 percent of all calls would be connected right away. In 1909, Erlang published a paper with his findings, creating a new branch of mathematics called queueing theory.

Today, queueing theory finds use in many different places. Corporations with call centers, for instance, may often use the tenets of queueing theory to handle customer problems. The most basic problems, which are common, are handled by relatively unskilled but numerous representatives. More complex problems are passed up to a fewer number of people with more training. To determine the optimal number of each type of representative, a call center can use Erlang’s findings and not, as is commonly believed, a random number determined by the prince of darkness.

So back to those jerks at the supermarket who made it out ahead of you. Queueing theory explains why there’s probably no way you can always be in the fastest line. A grocery store tries to have enough employees at the checkout lines to get all their customers through with minimum delay. But sometimes, like on a Sunday afternoon, they get super busy. Because most grocery stores don’t have the physical space to add more checkout lines, their system becomes overwhelmed. Some small interruption—a price check, a particularly talkative customer—will have downstream effects, holding up the entire line behind them.

If there are three lines at the store, these delays will happen randomly at different registers. Think about the probability. The chances of your line being that fastest one are only one in three. Which means you have a two-thirds chance of not being in the fastest line. So it’s not just in your mind: Another line is probably moving faster than yours.

Now, queueing theorists have come up with a good solution to this problem: Just make all customers stand in one long snaking line, called a serpentine line, and serve each person at the front with the next available register. With three registers, this method is about three times faster on average than the more traditional approach. This is what they do at most banks, Trader Joe's, and some fast-food places. With a serpentine line, a long delay at one register won't unfairly punish the people who lined up behind it. Instead, it will slow everyone down a little bit.

So why don’t most places encourage serpentine lines? Here, we’re getting into customer psychology. We human beings like to think that we’re in control of our lives and can beat the system if given the chance. Researchers have noted that some customers balk at serpentine lines, which can stretch much longer than the more traditional approach, preferring their chances of winning the lottery with multiple lines.

Queueing theory has grown to more than just math, incorporating these psychological aspects to waiting in line. The reason that elevator lobbies often have floor-to-ceiling mirrors is that they help alleviate the boredom of waiting for the next lift. Lines at an amusement park like Disneyland incorporate all sorts of diversions—like changing backgrounds, progression through different rooms, and video screens—to keep park-goers preoccupied and feeling like they are making progress toward a goal while standing for two hours to get on a five-minute ride. Smart phones are probably the greatest boon to modern line designers. Pretty much anyone can now kill time by playing games, checking social media, or browsing the internet while waiting.

Finally, just to prove that the most rational choice isn’t always the best one, there’s this amusing anecdote from prominent queueing researcher Richard Larson of MIT. During a queueing theory conference, Larson said that a hotel lobby was once clogged with queueing theorists attempting to check in to their rooms. The mathematicians decided to take matters into their own hands and form a serpentine line to handle the volume.

But, as Larson told Slate in 2012: "The lobby wasn’t designed for it and it looked extremely messy. The hotel manager was unhappy. If we’d just dispersed into six parallel lines at the checkout desk the wait might have been shorter and less chaotic. But it would have been less fair."

凌哥简介

教育硕士

高级教师

英语研训员

国培专家

桐乡翻译学会理事

【 讲座 · 出版 · 发表 】

浙江大学、浙江师范大学、杭州师范大学、浙江外国语学院、云南师范大学、杭州电子科技大学、湖州师范学院、丽水学院、金华教育学院、温州教师教育院、嘉兴教育学院、陕西安康学院；小学英语教研员与名师国培班、湖南省小学英语骨干教师培训班、江浙沪三地小学英语教师联盟；杭州师范大学教师教育学院网络课程、腾讯课堂、一起云端教育论坛；广西南宁市、青海德令哈市、四川青川县、宁夏永宁县；杭州市（下城区、西湖区、拱墅区、江干区、余杭区、临安、富阳），嘉兴市（南湖、秀洲、嘉善、平湖、海盐、海宁、桐乡），湖州市（南浔区、德清县），绍兴市（柯桥区），宁波市（镇海区、江北区）；台州市（黄岩区、温岭市、仙居县）；金华市（婺城区、义乌市、兰溪市、东阳市）；丽水市（缙云、云和、景宁、松阳、龙泉）；衢州市（柯城区）；温州市（鹿城区、永嘉县、苍南县、泰顺县、洞头县）。中国教师研修网、中国教师教育网、前沿课堂、杰尔特国际英语教学论坛、清瑞教育科技、一起作业网、弘育科技。上海外语教育出版社、浙江教育出版社、浙江工商大学出版社、中国原子能出版社。《中小学外语教学》、《中小学英语教学与研究》、《小学教学设计·英语》、《英语周报》、《英语辅导报》、《浙江教育报》。